MCS
The Recommended Publication for Citing
- Hyunsuk Lee, Wonkyeong Kim, Peng Zhang, Azamat Khassenov, Yunki Jo, Jinsu Park, Jiankai Yu, Matthieu Lemaire, Deokjung Lee*, “MCS – A Monte Carlo Particle Transport Code for Large-Scale Power Reactor Analysis,” Annals of Nuclear Energy, 139: 107276. https://doi.org/10.1016/j.anucene.2019.107276 (2020)
- Yunki Jo, Deokjung Lee*, “Current Capabilities and Future Developments of Monte Carlo Code MCS,” EPJ Nuclear Sci. Technol., Under Review (2024)
- Eun Jeong, Deokjung Lee*, “Development Status of MCSTD-GPU: GPU-based Monte Carlo Time-dependent Code for Reactor Transient Analysis,” ANS Winter Conference and Expo 24, Orlando FL, USA, November 17-21 (2024)
Introduction
The Monte Carlo code, MCS was developed at the Ulsan National Institute of Science and Technology (UNIST) in 2011. In the initial development phase, the primary focus was on developing a Monte Carlo code for the high-fidelity multicycle analysis of large-scale power reactors, especially pressurized water reactors. For the power reactor analysis, capabilities including refueling and shuffling of fuel assemblies, on-the-fly Doppler broadening of neutron cross-sections, and multiphysics coupling were implemented in the MCS. Beyond reactor analysis and capabilities, MCS has been developed to extend its applications. The MCS has been used for radiation shielding, group constant generation, sensitivity, uncertainty, and transient analysis.
Overview
Monte Carlo Code MCS
• Language: Fortran 2003
• Purpose
– High-fidelity multicycle analysis of large-scale reactors with accelerated Monte Carlo simulation
– University research: MC methodology development, advanced reactor design
– University research: MC methodology development, advanced reactor design
• 3-D geometry using constructive solid geometry (CSG) system • Nuclear Data
– ENDF-B, JENDL, and JEFF
– Continuous energy and multi-group cross-section data
– Probability table method
– S(alpha,beta) thermal scattering
– Double indexing method• Physics
– Neutron and photon transport
– Resonance upscattering (DBRC, FESK)
– On-the-fly Doppler broadening and windowed multipole method
– Equilibrium xenon calculation
– Thermal/hydraulics calculation module, TH1D
– Soluble boron concentration and control rod position search capabilities for a target k-eigenvalue
– Adjoint-weighted point kinetics parameter calculation using an iterated fission probability (IFP) method
– Sensitivity calculation using a generalized perturbation theory (GPT)
– Uncertainty calculation using a sandwich rule
– Group constants generation for a two-step reactor analysis method
– Radiation shielding analysis with dose rate calculation
– Variance reduction technique using weight window method
– Time-dependent Monte Carlo simulation (TDMC)
– Functional expansion tally (FET)• Acceleration
– MOC and MC Hybrid solver
– Modified power iteration
– Wielandt method and super-history method
– CMFD• Parallelism
– MPI and OpenMP parallel simulation
– Parallel fission bank• Depletion
– CRAM, MEM, Krylov Subspace
– Predictor, semi-predictor-corrector, and full predictor-corrector methods
– Quadratic depletion model for gadolinium isotopes
– ENDF-B, JENDL, and JEFF
– Continuous energy and multi-group cross-section data
– Probability table method
– S(alpha,beta) thermal scattering
– Double indexing method• Physics
– Neutron and photon transport
– Resonance upscattering (DBRC, FESK)
– On-the-fly Doppler broadening and windowed multipole method
– Equilibrium xenon calculation
– Thermal/hydraulics calculation module, TH1D
– Soluble boron concentration and control rod position search capabilities for a target k-eigenvalue
– Adjoint-weighted point kinetics parameter calculation using an iterated fission probability (IFP) method
– Sensitivity calculation using a generalized perturbation theory (GPT)
– Uncertainty calculation using a sandwich rule
– Group constants generation for a two-step reactor analysis method
– Radiation shielding analysis with dose rate calculation
– Variance reduction technique using weight window method
– Time-dependent Monte Carlo simulation (TDMC)
– Functional expansion tally (FET)• Acceleration
– MOC and MC Hybrid solver
– Modified power iteration
– Wielandt method and super-history method
– CMFD• Parallelism
– MPI and OpenMP parallel simulation
– Parallel fission bank• Depletion
– CRAM, MEM, Krylov Subspace
– Predictor, semi-predictor-corrector, and full predictor-corrector methods
– Quadratic depletion model for gadolinium isotopes
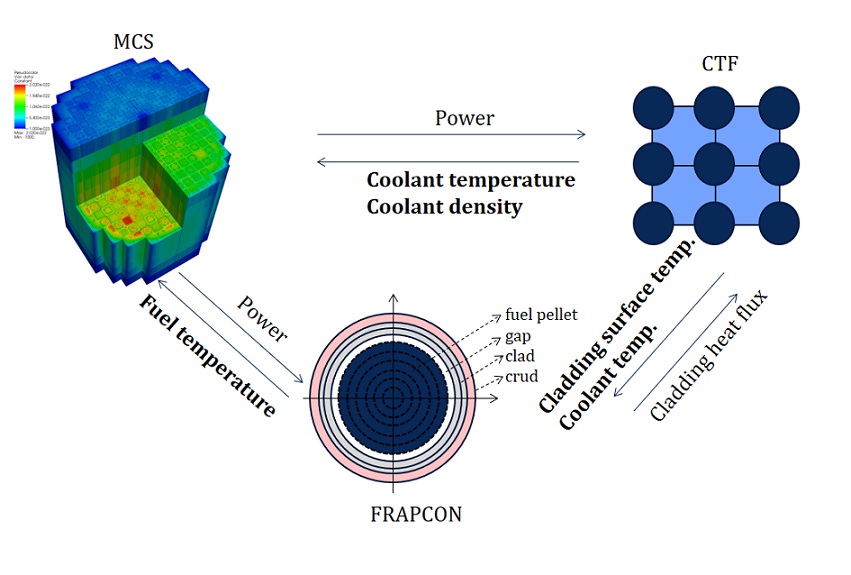
• Multi-physics coupling
– MCS/CTF
– MCS/FRAPCON
– MCS/CTF/FRAPCON
• Perturbation method
– Differential operator sampling (DOS)
– Correlated sampling (CS)
– Adjoint-weighted perturbation (AWP)
– Exact perturbation method using a perturbation-included iterated fission probability (PIFP) method
• Useful features
– Visualization of input and output
– C and Python preprocessing through input file
– Automatic cell division for depletion
– Sampling of particle distribution for stochastic geometry
– Monte Carlo based volume calculation function